地震地质 ›› 2023, Vol. 45 ›› Issue (4): 811-832.DOI: 10.3969/j.issn.0253-4967.2023.04.001
收稿日期:2022-08-10
修回日期:2022-11-22
出版日期:2023-08-20
发布日期:2023-09-20
作者简介:许建红, 男, 1983年生, 2022年于中国地震局地质研究所获构造地质学专业博士学位, 高级工程师, 主要从事活动构造研究、 地震安全性评价等工作, E-mail: xujianhongmailbox@163.com。
基金资助:
XU Jian-hong1,2)( ), CHEN Jie1), WEI Zhan-yu1), LI Tao1)
), CHEN Jie1), WEI Zhan-yu1), LI Tao1)
Received:2022-08-10
Revised:2022-11-22
Online:2023-08-20
Published:2023-09-20
摘要:
陡坎是一种自然界常见的台阶状地貌, 但其形成年龄通常很难直接测定。发育在松散堆积物中的陡坎经过初期短暂的重力垮塌之后, 将经历漫长的低能退化过程。如果陡坎剖面形态的演化可基于扩散方程来模拟, 且扩散系数可独立标定, 即可利用陡坎地形剖面估算其年龄, 这种方法被称为形貌测年。文中简要回顾了陡坎形貌测年的研究历史, 介绍并讨论了陡坎退化的概念模型与扩散模型, 特别是非线性扩散模型的建立及求解、 参数在扩散模型中所起的作用、 最佳陡坎形貌年龄的确定流程等, 分析了陡坎上、 下地貌面坡度对陡坎退化的影响, 编制了非线性扩散模型的年龄图版, 给出了图版的应用实例, 验证了形貌测年方法的有效性。线性扩散模型和非线性扩散模型均可用于单次事件陡坎的退化分析, 但对于年轻的单次事件陡坎推荐使用非线性扩散模型。断层重复活动形成的陡坎的退化分析则需要谨慎对待, 恒定滑动速率陡坎的非线性扩散模型适用于模拟年龄<10ka、 活动速率高的断层陡坎的演化; 多次事件陡坎模型(包括线性扩散和非线性扩散)需要仔细评估每次事件在陡坎剖面上的断错位置及其位移量。尽管陡坎形貌测年方法存在很多假设条件, 但目前快速获取一定范围内的高分辨率地形数据已成为现实, 从这些数据中可以沿着同一陡坎提取大量剖面进行分析, 继而得到具有统计意义的结果, 这为陡坎退化分析和形貌测年方法提供了广阔的应用前景。
许建红, 陈杰, 魏占玉, 李涛. 基于扩散方程的陡坎形貌测年方法进展[J]. 地震地质, 2023, 45(4): 811-832.
XU Jian-hong, CHEN Jie, WEI Zhan-yu, LI Tao. MORPHOLOGIC DATING OF SCARP MORPHOLOGY BASED ON DIFFUSION EQUATION: A REVIEW[J]. SEISMOLOGY AND GEOLOGY, 2023, 45(4): 811-832.
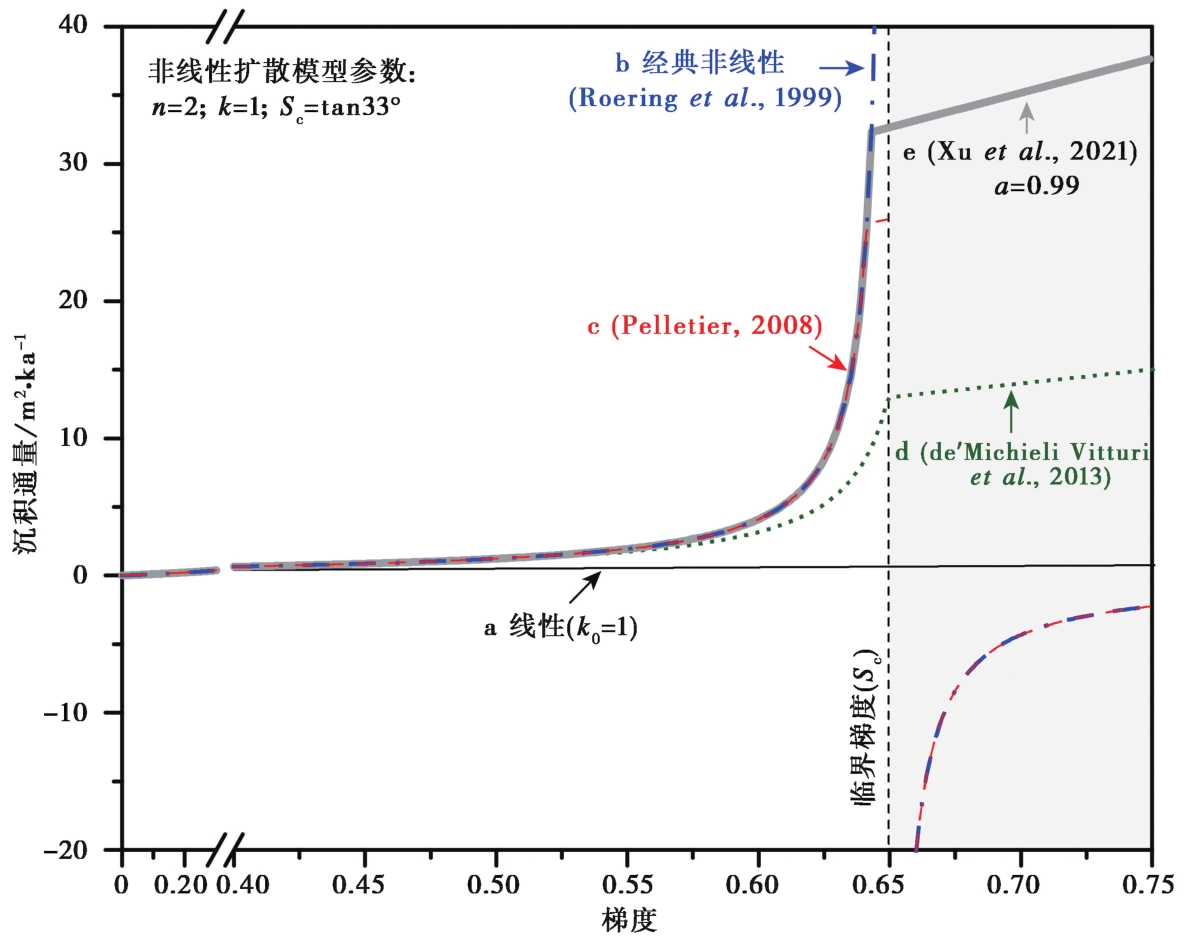
图 2 陡坎地形梯度和沉积通量之间的理论关系(Xu et al., 2021) a 线性关系(黑色细实线)(Hanks et al., 1984); b 经典非线性关系(蓝色点划线)(Roering et al., 1999)。当地形梯度接近临界梯度时, 沉积通量趋于无限大, 超过临界梯度时, 沉积通量变为负值; c Pelletier(2008)改进的非线性关系(在其公式中取Cmax=40, 红色虚线), 可避免无限通量, 但没有解决负值的问题; d de' Michieli Vitturi等(2013)改进的非线性关系(在其公式中取Cmax=20, 绿色点线), 虽可同时避免无限通量和负值, 但指数曲线段偏离了经典的非线性关系; e 适用于数值计 算的非线性关系(灰色粗实线)(Xu et al., 2021)
Fig. 2 Relationship between hillslope gradient and sediment flux(Xu et al., 2021).
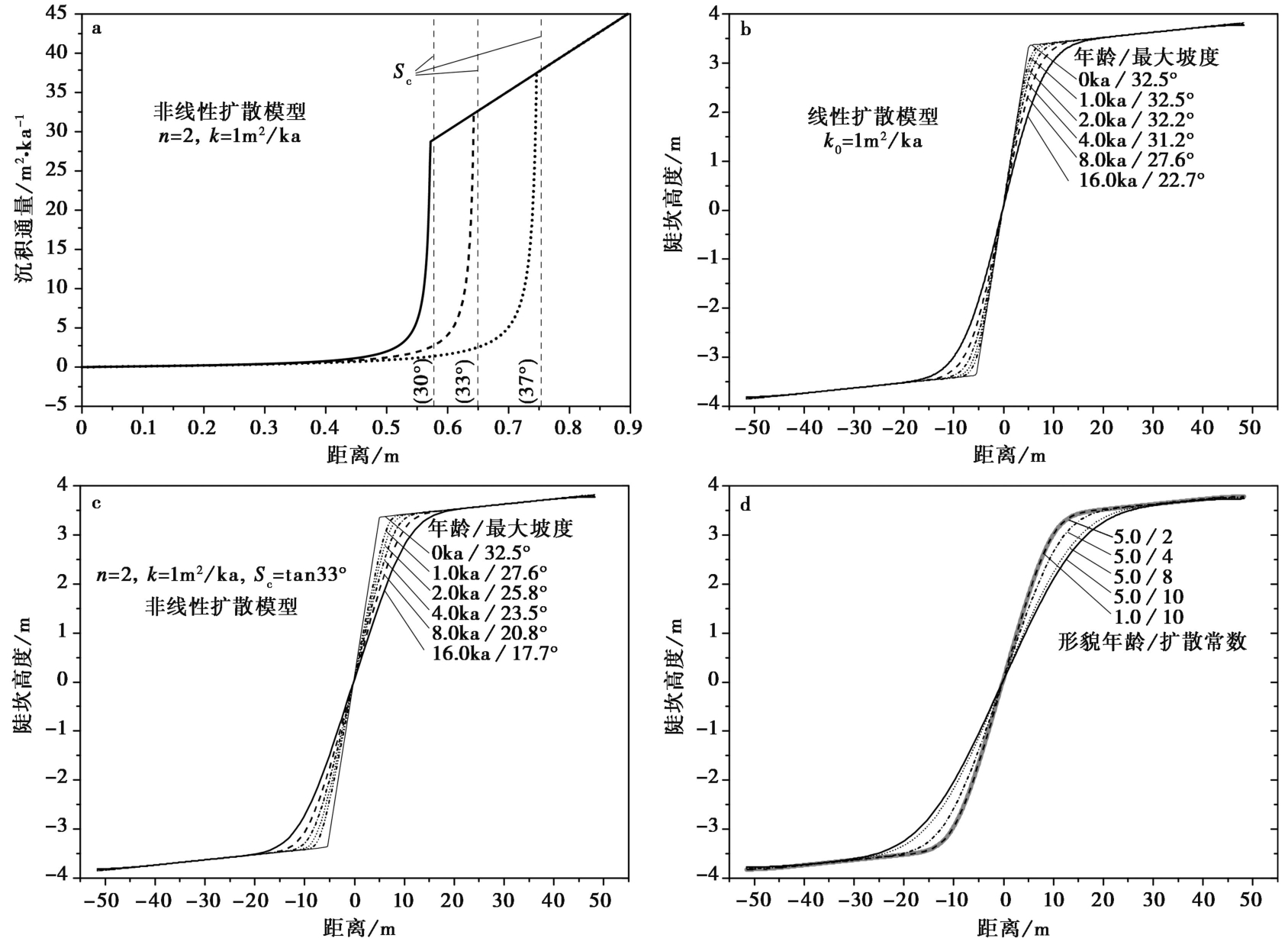
图 3 扩散模型中的参数变化对模型输出的影响(Xu et al., 2021) a 对于非线性扩散模型, 随着临界梯度增大, 沉积通量由小变大的转换位置对应的梯度也会增大; b 对于线性扩散模型, 侵蚀和堆积分别集中在陡坎的肩部和坡脚。当陡坎年龄t<4ka, 陡坎最大坡度几乎没有变化, 随着陡坎年龄增加至t>4ka, 其最大坡度才逐渐变小; c 对于非线性扩散模型, 侵蚀和堆积仍分别集中在陡坎的肩部和坡脚, 其最大坡度从一开始就随时间逐渐变小; d 对于不同的扩散常数k, 经过相同的演化时间之后, 更大的k值对应更明显的陡坎肩部侵蚀和坡脚堆积。然而,如果k·t的值相等, 陡坎剖面的最终形态相同, 与k和t各自的大小无关
Fig. 3 The influence of parameter changes on scarp evolution within diffusion models(Xu et al., 2021).
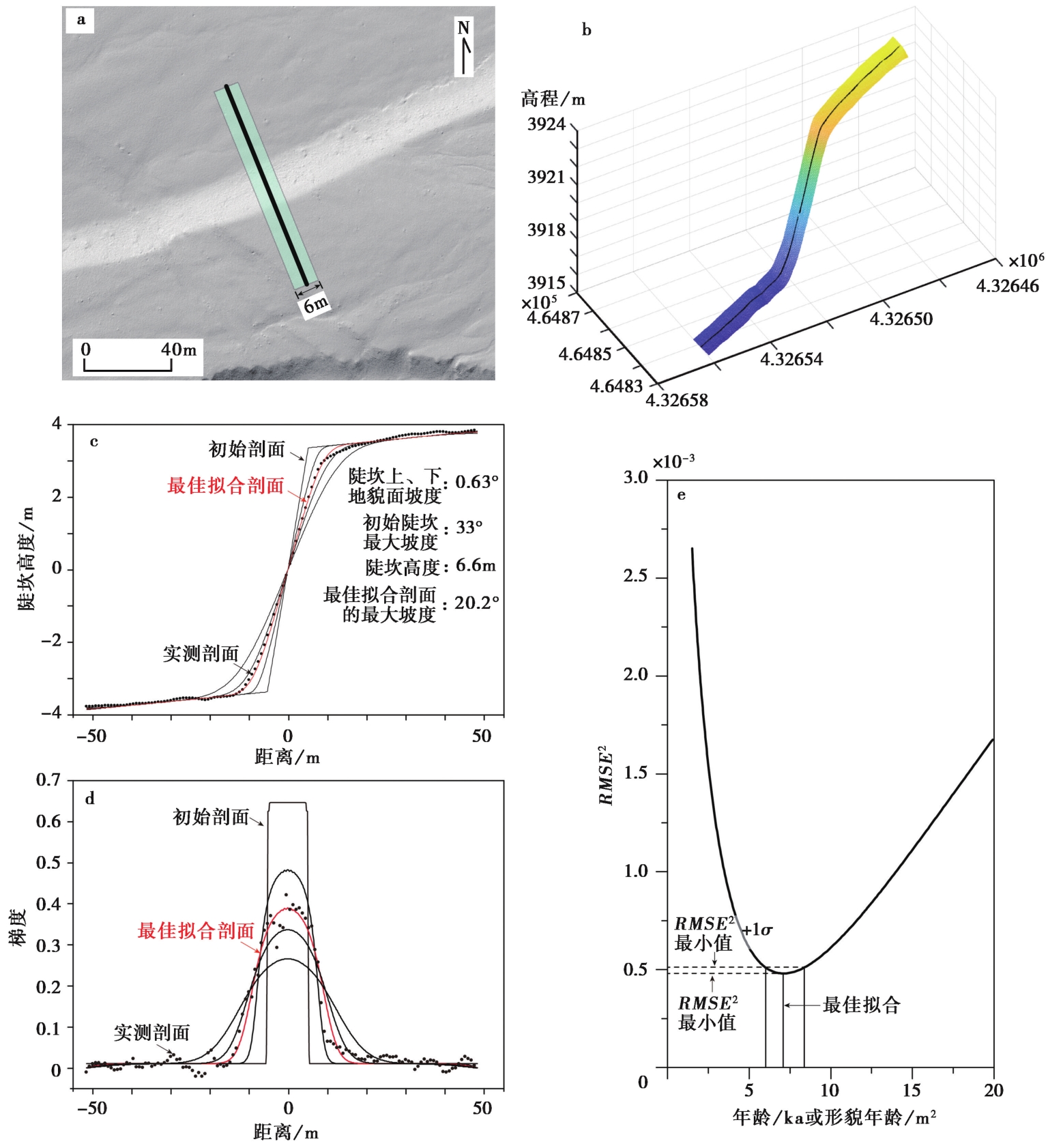
Fig. 4 基于DEM提取的条带状剖面确定陡坎年龄的流程(Wei et al., 2015) The scheme for exploiting DEM to conduct swath profile-based morphologic dating(Wei et al., 2015).a DEM栅影图可用于识别陡坎和确定陡坎剖面的位置。黑线代表条带状剖面的中线, 图中标记的为6m宽的DEM条带; b 从DEM数据中提取的条带状剖面的三维视图。将条带内所有栅格点投影到黑色中线上; c 实测陡坎距离-高度剖面和不同时间节点模拟得到的陡坎距离-高度剖面。黑色点代表的剖面对应图b中的条带状DEM剖面。黑色和红色细线代表不同时间节点的模拟剖面, 其中红线代表了最佳模拟剖面; d 在时间为t的范围内模拟陡坎的梯度剖面, 与图c中的剖面对应, 红色的梯度剖面代表最佳拟合结果; e 实测梯度剖面与模拟梯度剖面之间的均方根误差。中间的竖线代表由最小RMSE2确定的最佳年龄t(实际年龄(ka)或形貌年龄(m2)), 两侧的竖线则代表了由卡方分布确定的1个标准差
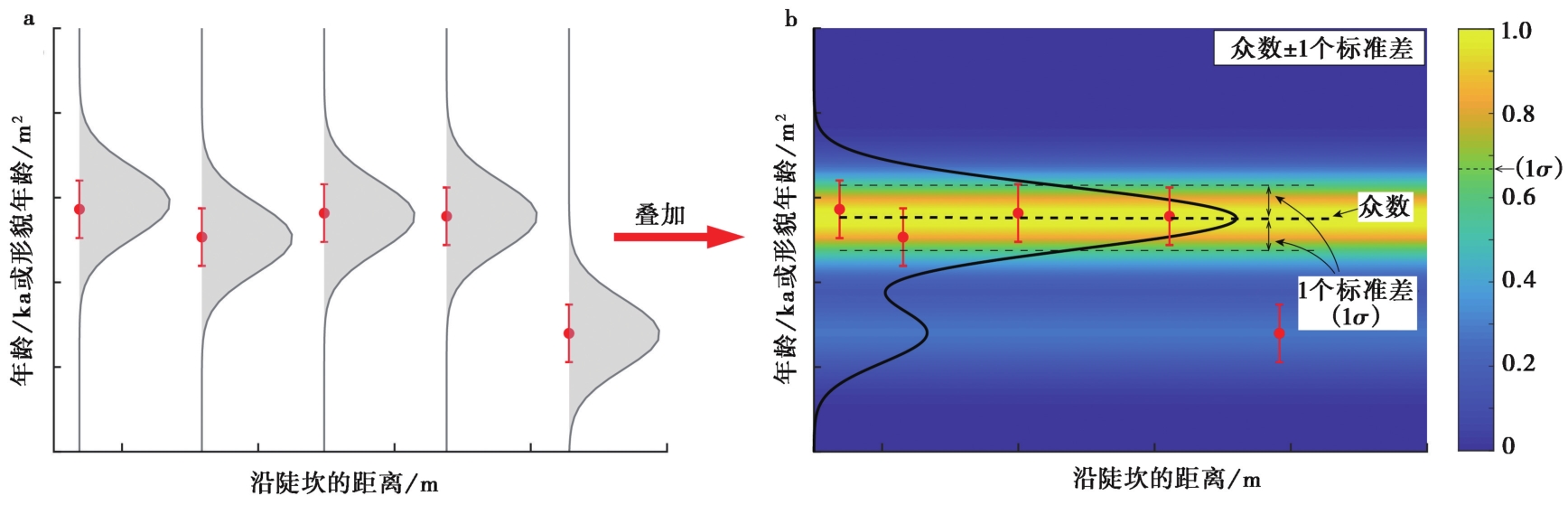
图 5 用于识别数据丛集的累积概率密度(CPD)方法 a 沿陡坎不同距离上的剖面(通常间距数米至几十米)限定的陡坎年龄(实际年龄(ka)或形貌年龄(m2))的概率密度分布, 带误差棒的红色圆点代表了陡坎年龄和1个标准差; b 叠加陡坎年龄的概率密度分布可以得到累积概率密度分布图, 从中可以确定具有统计意义的陡坎年龄, 即概率最大值和标准差, 标准差可以反映数据的集中度。右侧的颜色棒(Color bar)中标示了不同概率对应的颜色, 1个标准差大体对应由蓝色向黄色转变的位置
Fig. 5 Identifying clusters of data using the Cumulative Probability Density(CPD)method.
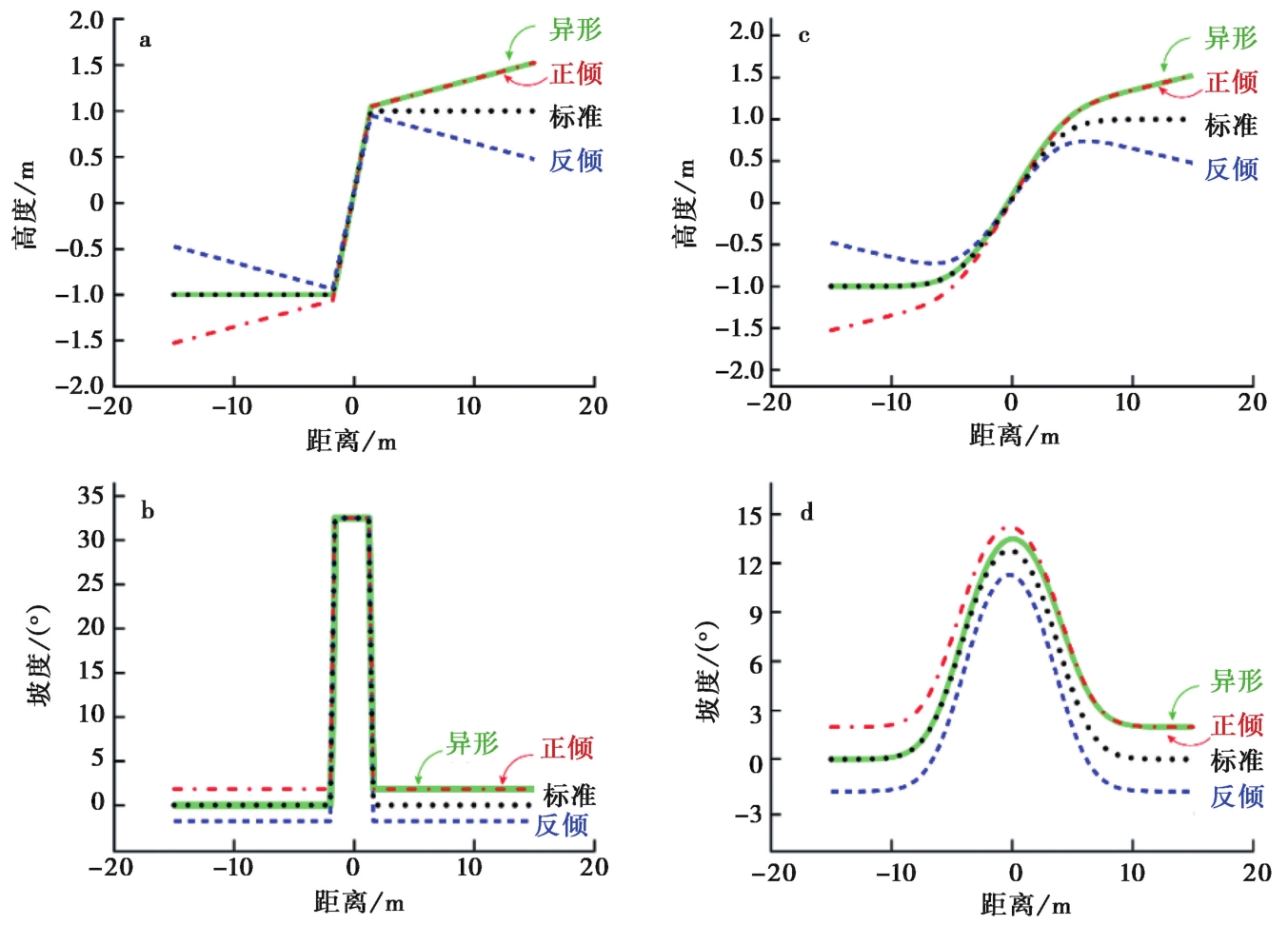
图 6 陡坎上、 下地貌面的坡度对陡坎退化的影响 左侧为初始状态下的陡坎高度(a)和坡度剖面(b), 右侧为退化一定时间后的陡坎高度(c)和坡度剖面(d)。与上、 下地貌面水平的剖面(标准)相比, 当上、 下地貌面的坡向与陡坎倾向一致时, 会整体抬高陡坎坡度值(正倾); 当上、 下地貌面的坡向与陡坎倾向相反时, 会整体降低坡度值(反倾); 上、 下地貌面倾斜程度不同的剖面(异形),坡度变化的幅度约等于上、 下地貌面坡度的平均值
Fig. 6 Effect of far-field slope on scarp degradation.
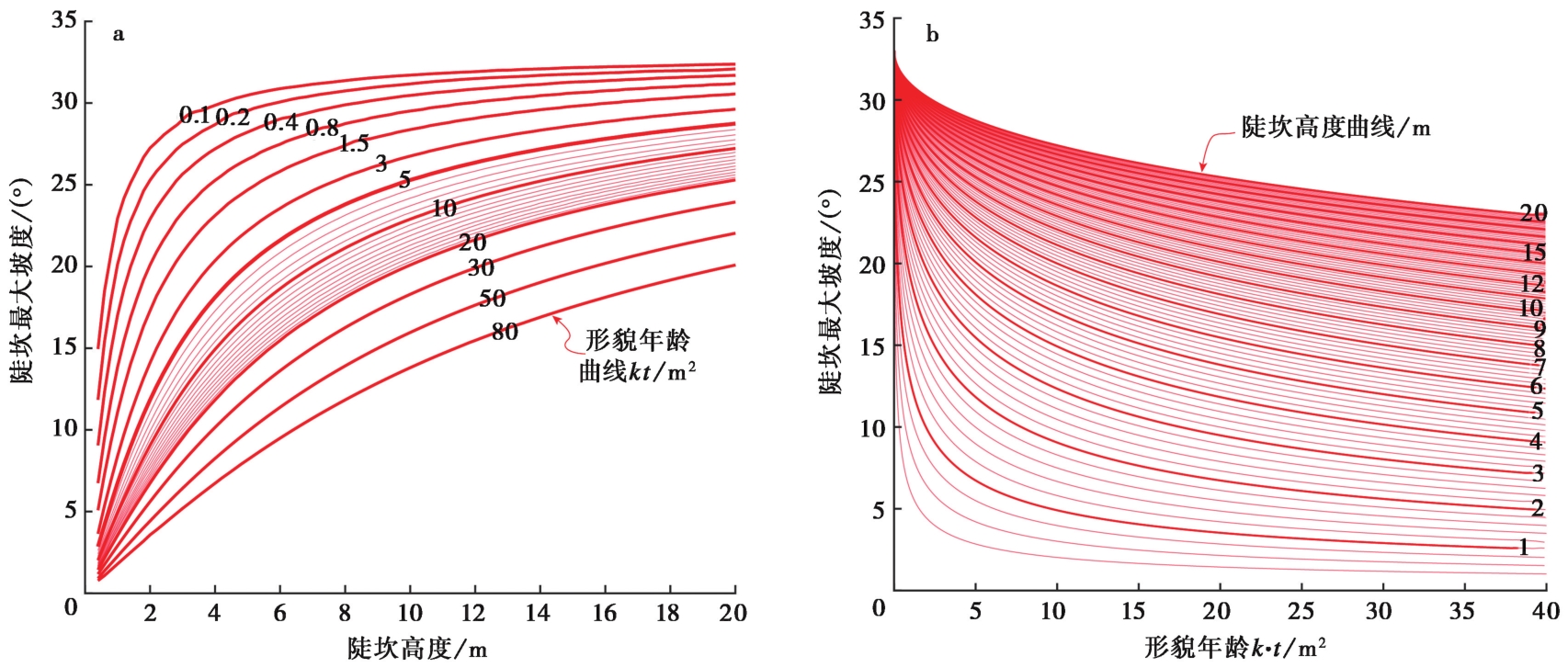
图 7 陡坎非线性扩散模型的年龄图版 a 高度-最大坡度图版; b 年龄-最大坡度图版。使用非线性扩散模型制作图版, 模型参数分别为:临界梯度Sc=tan33°, 非线性指数n=2, 扩散常数k=1m2/ka
Fig. 7 Scarp age pattern of nonlinear diffusion model.
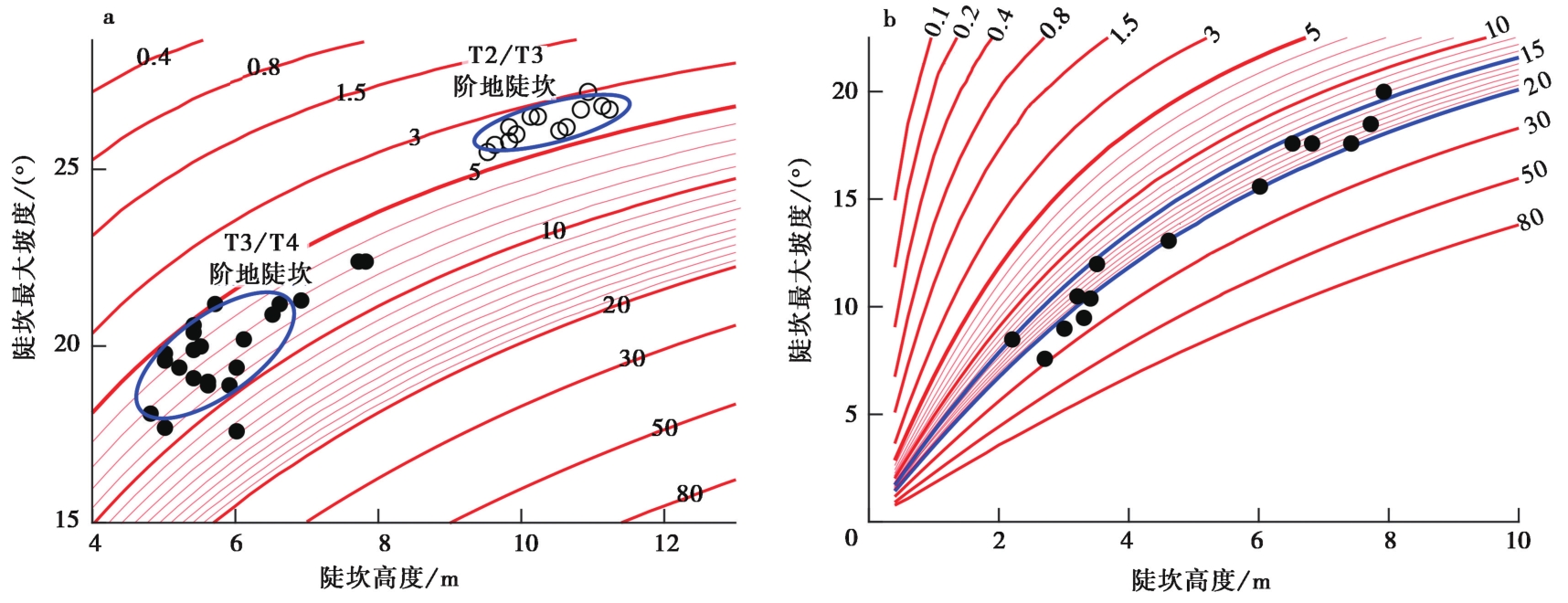
Fig. 8 示例已有研究成果 Examples of existing research results.a 中国西部帕米尔高原木吉盆地内齐姆干河出山口处阶地陡坎的数据, 图版完全可以区分2级高度不同的阶地陡坎; b 美国博纳维尔(Bonneville)湖岸线陡坎的数据, 沿同一陡坎不同高度的陡坎剖面限定的形貌年龄很好地集中在15~20m2。图中 实心圆和空心圆分别代表沿陡坎不同位置的陡坎高度和最大坡度值(图b考虑了陡坎上、 下地貌面的坡度)
| 断错 次数 | Δh=0.2m, Δt=2ka, θf=2° | Δh=0.5m, Δt=2.5ka, θf=2° | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H | Rage | Mage | Mφ | Ratio | H | Rage | Mage | Mφ | Ratio | ||
| 1 | 0.2 | 2 | 2 | 4.3 | 1.0 | 0.5 | 2.5 | 2.5 | 5.9 | 1.0 | |
| 2 | 0.4 | 4 | 3.1 | 5.7 | 0.8 | 1 | 5 | 3.5 | 8.7 | 0.7 | |
| 3 | 0.6 | 6 | 4.2 | 6.7 | 0.7 | 1.5 | 7.5 | 4.4 | 10.7 | 0.6 | |
| 4 | 0.8 | 8 | 5 | 7.5 | 0.6 | 2 | 10 | 5.1 | 12.4 | 0.5 | |
| 5 | 1 | 10 | 5.8 | 8.3 | 0.6 | 2.5 | 12.5 | 6 | 13.6 | 0.5 | |
| 8 | 1.6 | 16 | 8.2 | 10.0 | 0.5 | 4 | 20 | 8.2 | 16.4 | 0.4 | |
| 10 | 2 | 20 | 9.7 | 10.9 | 0.5 | 5 | 25 | 9.6 | 17.6 | 0.4 | |
| 16 | 3.2 | 32 | 14.2 | 12.9 | 0.4 | 8 | 40 | 13.6 | 20.2 | 0.3 | |
表 1 重复活动断层陡坎的“形貌年龄”与实际年龄对比
Table 1 Comparison of morphologic age and the actual age of repeated active fault scarps<br
| 断错 次数 | Δh=0.2m, Δt=2ka, θf=2° | Δh=0.5m, Δt=2.5ka, θf=2° | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H | Rage | Mage | Mφ | Ratio | H | Rage | Mage | Mφ | Ratio | ||
| 1 | 0.2 | 2 | 2 | 4.3 | 1.0 | 0.5 | 2.5 | 2.5 | 5.9 | 1.0 | |
| 2 | 0.4 | 4 | 3.1 | 5.7 | 0.8 | 1 | 5 | 3.5 | 8.7 | 0.7 | |
| 3 | 0.6 | 6 | 4.2 | 6.7 | 0.7 | 1.5 | 7.5 | 4.4 | 10.7 | 0.6 | |
| 4 | 0.8 | 8 | 5 | 7.5 | 0.6 | 2 | 10 | 5.1 | 12.4 | 0.5 | |
| 5 | 1 | 10 | 5.8 | 8.3 | 0.6 | 2.5 | 12.5 | 6 | 13.6 | 0.5 | |
| 8 | 1.6 | 16 | 8.2 | 10.0 | 0.5 | 4 | 20 | 8.2 | 16.4 | 0.4 | |
| 10 | 2 | 20 | 9.7 | 10.9 | 0.5 | 5 | 25 | 9.6 | 17.6 | 0.4 | |
| 16 | 3.2 | 32 | 14.2 | 12.9 | 0.4 | 8 | 40 | 13.6 | 20.2 | 0.3 | |
| [1] |
邓起东, 尤惠川. 1985. 断层崖研究与地震危险性估计: 以贺兰山东麓断层崖为例[J]. 西北地震学报, 7(1): 29-38.
|
|
|
|
| [2] |
侯康明, 韩有珍, 张守杰. 1995. 断层崖形成年代的数学模拟计算[J]. 西北地震学报, 17(2): 68-75, 81.
|
|
|
|
| [3] |
黄昭. 1987. 贺兰山东麓断层崖的形态与年代测定方法[G]//国家地震局地质研究所编. 现代地壳运动研究(3). 北京: 地震出版社: 63-82.
|
|
|
|
| [4] |
邱祝礼, 李有利, 南峰. 2005. 断层陡崖、 沟谷演化模型及三维可视化[J]. 水土保持研究, 12(4): 35-38, 84.
|
|
|
|
| [5] |
闫计明, 魏占玉, 何宏林. 2013. 黄土地区坡面侵蚀率的实验研究[J]. 地震地质, 35(4): 793-804. doi: 10.3969/j.issn.0253-4967.2013.04.009.
DOI |
|
|
|
| [6] |
尤惠川, 邓起东, 冉勇康. 2004. 断层崖演化与古地震研究[J]. 地震地质, 26(1): 33-45.
|
|
|
|
| [7] |
张培震, 李传友, 毛凤英. 2008. 河流阶地演化与走滑断裂滑动速率[J]. 地震地质, 30(1): 44-57.
|
|
|
|
| [8] |
DOI URL |
| [9] |
DOI URL |
| [10] |
DOI |
| [11] |
DOI |
| [12] |
DOI |
| [13] |
DOI URL |
| [14] |
DOI |
| [15] |
|
| [16] |
DOI URL |
| [17] |
DOI URL |
| [18] |
DOI |
| [19] |
DOI URL |
| [20] |
DOI URL |
| [21] |
DOI URL |
| [22] |
DOI URL |
| [23] |
de' Michieli Vitturi M,
DOI |
| [24] |
DOI |
| [25] |
|
| [26] |
DOI |
| [27] |
DOI |
| [28] |
|
| [29] |
DOI URL |
| [30] |
|
| [31] |
|
| [32] |
DOI |
| [33] |
DOI |
| [34] |
DOI URL |
| [35] |
DOI URL |
| [36] |
DOI |
| [37] |
DOI URL |
| [38] |
DOI URL |
| [39] |
DOI |
| [40] |
DOI URL |
| [41] |
|
| [42] |
DOI URL |
| [43] |
DOI URL |
| [44] |
DOI URL |
| [45] |
|
| [46] |
DOI URL |
| [47] |
DOI URL |
| [48] |
DOI |
| [49] |
DOI |
| [50] |
|
| [51] |
DOI URL |
| [52] |
DOI URL |
| [53] |
DOI URL |
| [54] |
DOI |
| [55] |
DOI URL |
| [56] |
DOI URL |
| [57] |
|
| [58] |
DOI URL |
| [59] |
|
| [60] |
DOI URL |
| [61] |
DOI URL |
| [62] |
DOI URL |
| [63] |
DOI URL |
| [64] |
DOI PMID |
| [65] |
DOI URL |
| [1] | 李安, 万波, 王晓先, 计昊旻, 索锐. 金州断裂盖州北鞍山段古地震破裂的新证据[J]. 地震地质, 2023, 45(1): 111-126. |
| [2] | 郑海刚, 姚大全, 赵朋, 杨源源, 黄金水. 郯庐断裂带赤山段全新世新活动的特征[J]. 地震地质, 2023, 45(1): 127-138. |
| [3] | 张伟恒, 陈杰, 李涛, 邸宁, 姚远. 龙门山前陆冲断带南段三苏场背斜晚第四纪变形速率[J]. 地震地质, 2022, 44(6): 1351-1364. |
| [4] | 黄帅堂, 常想德, 马建, 胡伟华, 任静, 刘建明, 张文秀, 赖爱京. 天山北麓库松木契克山山前断裂东段断层陡坎研究[J]. 地震地质, 2022, 44(1): 20-34. |
| [5] | 苗树清, 胡宗凯, 张玲, 杨海波, 杨晓平. 洪积扇顶部活动走滑断裂的断错地貌分析——以新疆塔城盆地东缘阿合别斗河冲洪积扇为例[J]. 地震地质, 2021, 43(3): 488-503. |
| [6] | 许建红, 惠旭辉, 程宏宾, 张晓亮, 尚思歧. 柴达木盆地西南缘油砂山断裂的古地震和晚第四纪活动速率[J]. 地震地质, 2018, 40(2): 465-479. |
| [7] | 雷惊昊, 李有利, 胡秀, 辛伟林, 熊建国, 钟岳志. 东大河阶地陡坎对民乐-大马营断裂垂直滑动速率的指示[J]. 地震地质, 2017, 39(6): 1256-1266. |
| [8] | 田勤虎, 周本刚, 李晓妮, 石金虎, 魏青珂, 卞菊梅. 渭河断裂杨家村-窑店段展布及晚第四纪活动特征[J]. 地震地质, 2016, 38(1): 141-151. |
| [9] | 张玲, 杨晓平, 黄伟亮, 李胜强. 褶皱陡坎中相关断层在缩短量计算中的作用——以东秋里塔格背斜为例[J]. 地震地质, 2015, 37(3): 697-708. |
| [10] | 李涛, 陈杰, 肖伟鹏. 滑脱褶皱陡坎的变形特征和运动学模型:以帕米尔-南天山前陆地区明尧勒背斜为例[J]. 地震地质, 2014, 36(3): 677-691. |
| [11] | 李涛, 陈杰. 利用河流阶地限定活动逆断层相关褶皱晚第四纪变形机制和速率:方法与认识[J]. 地震地质, 2014, 36(2): 478-488. |
| [12] | 杨晓东, 陈杰, 李涛, 李文巧, 刘浪涛, 杨会丽. 塔里木西缘明尧勒背斜的弯滑褶皱作用与活动弯滑断层陡坎[J]. 地震地质, 2014, 36(1): 14-27. |
| [13] | 刘玉刚, 陈涛, 闵伟, 周本刚. 苍山-尼山断裂西段第四纪晚期活动性[J]. 地震地质, 2013, 35(4): 754-764. |
| [14] | 陈涛, 刘玉刚, 闵伟, 周本刚. 塔尔湾断裂活动时代厘定及地貌陡坎成因分析[J]. 地震地质, 2012, (3): 401-414. |
| [15] | 许建红, 谢新生, 孙昌斌. 山西罗云山山前断裂带中段龙祠-峪口全新世活动证据[J]. 地震地质, 2011, 33(4): 855-864. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||