地震地质 ›› 2024, Vol. 46 ›› Issue (4): 934-954.DOI: 10.3969/j.issn.0253-4967.2024.04.010
李志恒1,2)( ), 谢俊举1),*(
), 谢俊举1),*( ), 李柯苇1,3), 温增平1), 李小军4), 王志才2), 许洪泰2), 赵晓芬1), 张娜1)
), 李柯苇1,3), 温增平1), 李小军4), 王志才2), 许洪泰2), 赵晓芬1), 张娜1)
收稿日期:2023-07-06
修回日期:2023-12-09
出版日期:2024-08-20
发布日期:2024-09-23
通讯作者:
谢俊举
作者简介:李志恒, 男, 1990年生, 2018年于中国地质大学(北京)获地质工程专业硕士学位, 工程师, 主要从事工程地震方面的研究, E-mail: leezh87@163.com。
基金资助:
LI Zhi-heng1,2)( ), XIE Jun-ju1),*(
), XIE Jun-ju1),*( ), LI Ke-wei1,3), WEN Zeng-ping1), LI Xiao-jun4), WANG Zhi-cai2), XU Hong-tai2), ZHAO Xiao-fen1), ZHANG Na1)
), LI Ke-wei1,3), WEN Zeng-ping1), LI Xiao-jun4), WANG Zhi-cai2), XU Hong-tai2), ZHAO Xiao-fen1), ZHANG Na1)
Received:2023-07-06
Revised:2023-12-09
Online:2024-08-20
Published:2024-09-23
Contact:
XIE Jun-ju
摘要:
场地剪切波速是进行场地分类和定量估计场地对地震动影响的重要参数, 在工程抗震设防和震后震害快速评估等方面具有广泛应用。文中利用山东地区1 336个工程场地的剪切波速剖面数据, 分别基于常速度外推方法、 速度梯度外推方法和条件独立方法建立了山东地区场地剪切波速VS20 和VS30 的经验外推模型。研究结果表明, 常速度外推方法对较浅的钻孔进行波速外推时会产生明显的低估, 且预测误差较大。速度梯度外推方法的拟合结果表现出明显的区域性特征, 山东地区的VS30 预测结果与美国加州和北京平原地区的结果相比, 总体上较为接近, 但明显低于日本地区。综合考虑建立的3种区域外推模型的精度和预测误差, 文中建议优先采用基于条件独立方法建立的山东地区的VS20 和VS30 经验外推模型, 获得的波速外推结果可以较好地为山东地区场地分类提供依据。
李志恒, 谢俊举, 李柯苇, 温增平, 李小军, 王志才, 许洪泰, 赵晓芬, 张娜. 山东地区场地剪切波速经验外推模型及其适用性[J]. 地震地质, 2024, 46(4): 934-954.
LI Zhi-heng, XIE Jun-ju, LI Ke-wei, WEN Zeng-ping, LI Xiao-jun, WANG Zhi-cai, XU Hong-tai, ZHAO Xiao-fen, ZHANG Na. EMPIRICAL EXTRAPOLATION MODEL OF SITE SHEAR WAVE VELOCITY AND ITS APPLICABILITY IN SHANDONG PROVINCE[J]. SEISMOLOGY AND GEOLOGY, 2024, 46(4): 934-954.
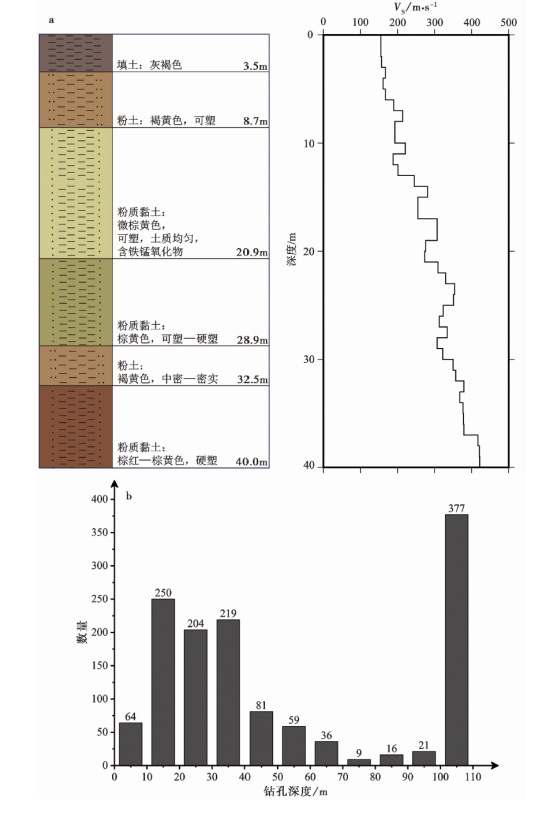
图 2 a 山东地区典型钻孔柱状图; b 不同深度钻孔数量分布图
Fig. 2 Histogram of typical boreholes in Shandong province(a) and distribution of the number of boreholes at different depths(b).
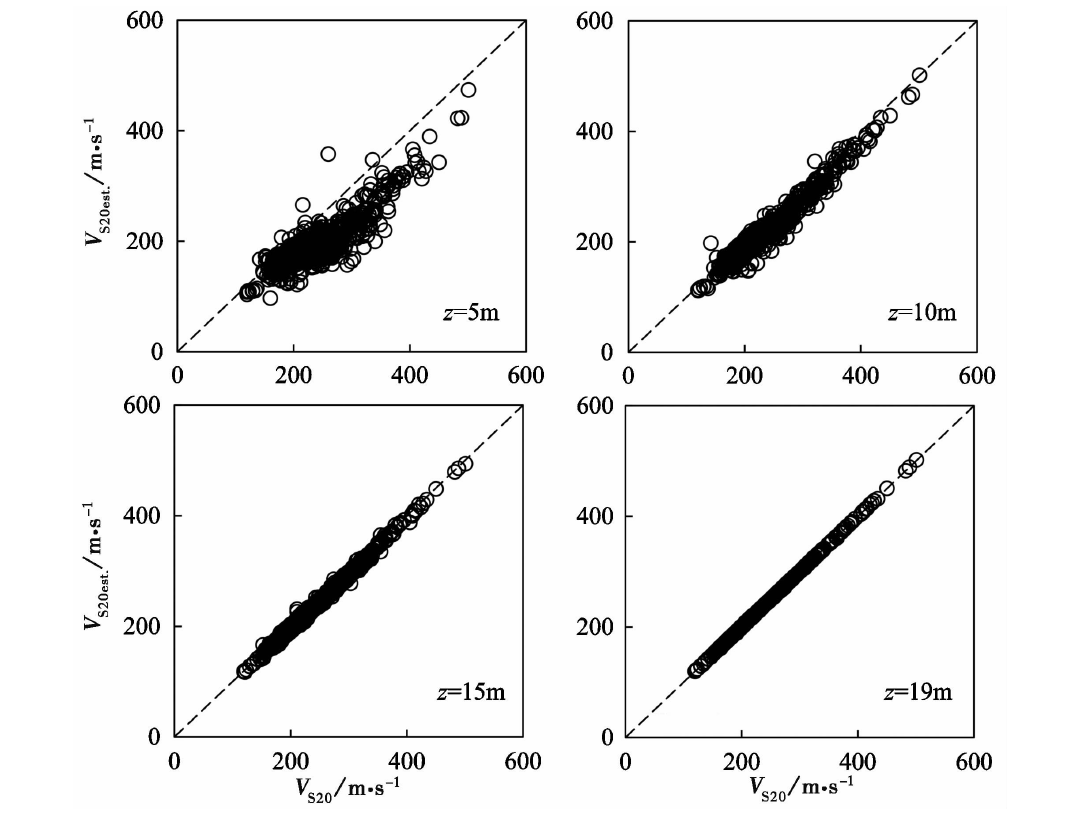
图 3 类比常速度外推方法的不同深度下预测值VS20est.与实测值VS20 对比
Fig. 3 Comparison of predicted VS20est. and measured VS20 at different depths based on the constant velocity extrapolation method.
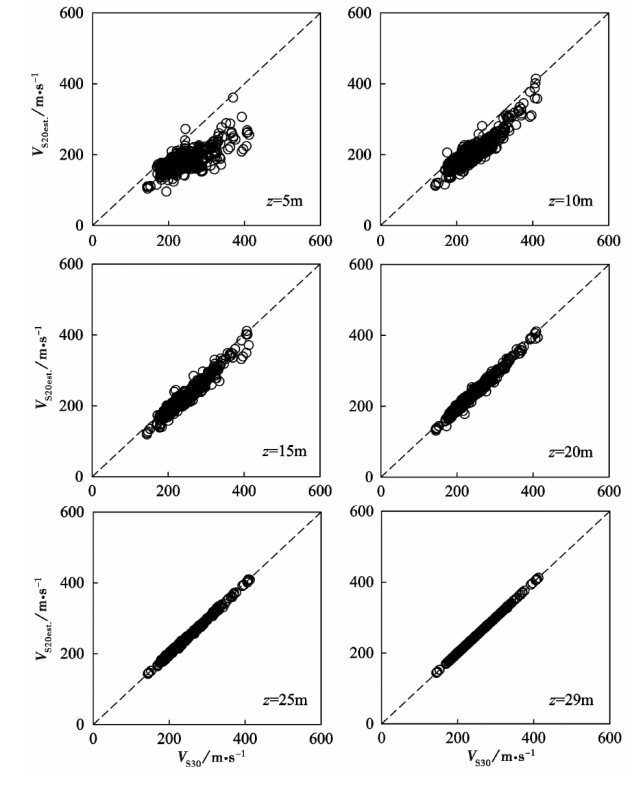
图 4 基于常速度外推方法的不同深度下预测值VS30est.与实测值VS30 的对比
Fig. 4 Comparison of predicted VS30est. and measured VS30 at different depths based on the constant velocity extrapolation method.
| 深度/m | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|
| 6 | 0.9232 | 1.0307 |
| 7 | 0.9395 | 0.8845 |
| 8 | 0.9610 | 0.7152 |
| 9 | 0.9739 | 0.5996 |
| 10 | 0.9820 | 0.4879 |
| 11 | 0.9878 | 0.3932 |
| 12 | 0.9902 | 0.3133 |
| 13 | 0.9937 | 0.2393 |
| 14 | 0.9952 | 0.1822 |
| 15 | 0.9979 | 0.1260 |
| 16 | 0.9984 | 0.0833 |
| 17 | 0.9994 | 0.0481 |
| 18 | 0.9998 | 0.0222 |
| 19 | 1.0000 | 0.0081 |
表1 类比常速度外推方法得到的VS20est.与VS20 之间的相关系数及预测误差标准差
Table1 Correlation coefficient and standard deviation of prediction error between VS20est. and VS20 obtained based on the constant velocity extrapolation method
| 深度/m | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|
| 6 | 0.9232 | 1.0307 |
| 7 | 0.9395 | 0.8845 |
| 8 | 0.9610 | 0.7152 |
| 9 | 0.9739 | 0.5996 |
| 10 | 0.9820 | 0.4879 |
| 11 | 0.9878 | 0.3932 |
| 12 | 0.9902 | 0.3133 |
| 13 | 0.9937 | 0.2393 |
| 14 | 0.9952 | 0.1822 |
| 15 | 0.9979 | 0.1260 |
| 16 | 0.9984 | 0.0833 |
| 17 | 0.9994 | 0.0481 |
| 18 | 0.9998 | 0.0222 |
| 19 | 1.0000 | 0.0081 |
| 深度/m | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|
| 6 | 0.8021 | 1.7491 |
| 7 | 0.8438 | 1.5863 |
| 8 | 0.8820 | 1.4086 |
| 9 | 0.9113 | 1.2879 |
| 10 | 0.9335 | 1.1414 |
| 11 | 0.9456 | 1.0356 |
| 12 | 0.9484 | 0.9256 |
| 13 | 0.9550 | 0.8221 |
| 14 | 0.9576 | 0.7308 |
| 15 | 0.9721 | 0.6250 |
| 16 | 0.9757 | 0.5381 |
| 17 | 0.9806 | 0.4649 |
| 18 | 0.9853 | 0.3826 |
| 19 | 0.9899 | 0.3286 |
| 20 | 0.9922 | 0.2650 |
| 21 | 0.9937 | 0.2017 |
| 22 | 0.9960 | 0.1508 |
| 23 | 0.9974 | 0.1098 |
| 24 | 0.9981 | 0.0793 |
| 25 | 0.9989 | 0.0557 |
| 26 | 0.9993 | 0.0372 |
| 27 | 0.9997 | 0.0223 |
| 28 | 0.9999 | 0.0127 |
| 29 | 1.0000 | 0.0044 |
表2 利用常速度外推方法得到的VS30est.与VS30 之间的相关系数及预测误差标准差
Table2 Correlation coefficient and standard deviation of prediction error between VS30est. and VS30 obtained using the constant velocity extrapolation method
| 深度/m | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|
| 6 | 0.8021 | 1.7491 |
| 7 | 0.8438 | 1.5863 |
| 8 | 0.8820 | 1.4086 |
| 9 | 0.9113 | 1.2879 |
| 10 | 0.9335 | 1.1414 |
| 11 | 0.9456 | 1.0356 |
| 12 | 0.9484 | 0.9256 |
| 13 | 0.9550 | 0.8221 |
| 14 | 0.9576 | 0.7308 |
| 15 | 0.9721 | 0.6250 |
| 16 | 0.9757 | 0.5381 |
| 17 | 0.9806 | 0.4649 |
| 18 | 0.9853 | 0.3826 |
| 19 | 0.9899 | 0.3286 |
| 20 | 0.9922 | 0.2650 |
| 21 | 0.9937 | 0.2017 |
| 22 | 0.9960 | 0.1508 |
| 23 | 0.9974 | 0.1098 |
| 24 | 0.9981 | 0.0793 |
| 25 | 0.9989 | 0.0557 |
| 26 | 0.9993 | 0.0372 |
| 27 | 0.9997 | 0.0223 |
| 28 | 0.9999 | 0.0127 |
| 29 | 1.0000 | 0.0044 |
| 深度/m | a0 | a1 | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|---|---|
| 6 | -0.4236 | 1.2317 | 0.8450 | 0.0533 |
| 7 | -0.4369 | 1.2336 | 0.8811 | 0.0472 |
| 8 | -0.4069 | 1.2160 | 0.9068 | 0.0420 |
| 9 | -0.3742 | 1.1976 | 0.9274 | 0.0373 |
| 10 | -0.3388 | 1.1781 | 0.9441 | 0.0329 |
| 11 | -0.2978 | 1.1565 | 0.9574 | 0.0288 |
| 12 | -0.2583 | 1.1357 | 0.9677 | 0.0251 |
| 13 | -0.2228 | 1.1168 | 0.9762 | 0.0216 |
| 14 | -0.1839 | 1.0968 | 0.9840 | 0.0178 |
| 15 | -0.1542 | 1.0807 | 0.9894 | 0.0145 |
| 16 | -0.1254 | 1.0652 | 0.9934 | 0.0114 |
| 17 | -0.0937 | 1.0486 | 0.9964 | 0.0084 |
| 18 | -0.0626 | 1.0323 | 0.9984 | 0.0057 |
| 19 | -0.0306 | 1.0158 | 0.9996 | 0.0028 |
表3 类比速度梯度法建立的山东地区VS20 经验预测模型回归分析结果
Table3 Regression analysis of the predictive empirical VS20 model based on the velocity gradient method in Shandong province
| 深度/m | a0 | a1 | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|---|---|
| 6 | -0.4236 | 1.2317 | 0.8450 | 0.0533 |
| 7 | -0.4369 | 1.2336 | 0.8811 | 0.0472 |
| 8 | -0.4069 | 1.2160 | 0.9068 | 0.0420 |
| 9 | -0.3742 | 1.1976 | 0.9274 | 0.0373 |
| 10 | -0.3388 | 1.1781 | 0.9441 | 0.0329 |
| 11 | -0.2978 | 1.1565 | 0.9574 | 0.0288 |
| 12 | -0.2583 | 1.1357 | 0.9677 | 0.0251 |
| 13 | -0.2228 | 1.1168 | 0.9762 | 0.0216 |
| 14 | -0.1839 | 1.0968 | 0.9840 | 0.0178 |
| 15 | -0.1542 | 1.0807 | 0.9894 | 0.0145 |
| 16 | -0.1254 | 1.0652 | 0.9934 | 0.0114 |
| 17 | -0.0937 | 1.0486 | 0.9964 | 0.0084 |
| 18 | -0.0626 | 1.0323 | 0.9984 | 0.0057 |
| 19 | -0.0306 | 1.0158 | 0.9996 | 0.0028 |
| 深度/m | a0 | a1 | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|---|---|
| 6 | -0.0249 | 1.0681 | 0.7233 | 0.0516 |
| 7 | -0.1169 | 1.1065 | 0.7668 | 0.0479 |
| 8 | -0.1767 | 1.1301 | 0.8047 | 0.0443 |
| 9 | -0.2202 | 1.1465 | 0.8370 | 0.0409 |
| 10 | -0.2400 | 1.1523 | 0.8649 | 0.0375 |
| 11 | -0.2385 | 1.1487 | 0.8874 | 0.0344 |
| 12 | -0.2227 | 1.1389 | 0.9043 | 0.0319 |
| 13 | -0.2034 | 1.1277 | 0.9181 | 0.0296 |
| 14 | -0.1706 | 1.1107 | 0.9300 | 0.0275 |
| 15 | -0.1605 | 1.1035 | 0.9409 | 0.0253 |
| 16 | -0.1493 | 1.0960 | 0.9499 | 0.0234 |
| 17 | -0.1360 | 1.0877 | 0.9578 | 0.0215 |
| 18 | -0.1222 | 1.0791 | 0.9648 | 0.0196 |
| 19 | -0.1101 | 1.0715 | 0.9716 | 0.0177 |
| 20 | -0.1005 | 1.0649 | 0.9774 | 0.0158 |
| 21 | -0.0935 | 1.0594 | 0.9824 | 0.0139 |
| 22 | -0.0858 | 1.0537 | 0.9866 | 0.0122 |
| 23 | -0.0800 | 1.0489 | 0.9900 | 0.0106 |
| 24 | -0.0723 | 1.0433 | 0.9927 | 0.0090 |
| 25 | -0.0632 | 1.0372 | 0.9950 | 0.0074 |
| 26 | -0.0530 | 1.0307 | 0.9969 | 0.0059 |
| 27 | -0.0416 | 1.0237 | 0.9983 | 0.0044 |
| 28 | -0.0291 | 1.0163 | 0.9992 | 0.0029 |
| 29 | -0.0155 | 1.0085 | 0.9998 | 0.0015 |
表 4 基于速度梯度法方法给出的山东地区VS30 经验外推关系回归分析结果
Table4 Results of regression analysis of VS30 empirical extrapolation relationships in Shandong province based on the velocity gradient method
| 深度/m | a0 | a1 | 皮尔逊相关系数r | 预测误差标准差σRES |
|---|---|---|---|---|
| 6 | -0.0249 | 1.0681 | 0.7233 | 0.0516 |
| 7 | -0.1169 | 1.1065 | 0.7668 | 0.0479 |
| 8 | -0.1767 | 1.1301 | 0.8047 | 0.0443 |
| 9 | -0.2202 | 1.1465 | 0.8370 | 0.0409 |
| 10 | -0.2400 | 1.1523 | 0.8649 | 0.0375 |
| 11 | -0.2385 | 1.1487 | 0.8874 | 0.0344 |
| 12 | -0.2227 | 1.1389 | 0.9043 | 0.0319 |
| 13 | -0.2034 | 1.1277 | 0.9181 | 0.0296 |
| 14 | -0.1706 | 1.1107 | 0.9300 | 0.0275 |
| 15 | -0.1605 | 1.1035 | 0.9409 | 0.0253 |
| 16 | -0.1493 | 1.0960 | 0.9499 | 0.0234 |
| 17 | -0.1360 | 1.0877 | 0.9578 | 0.0215 |
| 18 | -0.1222 | 1.0791 | 0.9648 | 0.0196 |
| 19 | -0.1101 | 1.0715 | 0.9716 | 0.0177 |
| 20 | -0.1005 | 1.0649 | 0.9774 | 0.0158 |
| 21 | -0.0935 | 1.0594 | 0.9824 | 0.0139 |
| 22 | -0.0858 | 1.0537 | 0.9866 | 0.0122 |
| 23 | -0.0800 | 1.0489 | 0.9900 | 0.0106 |
| 24 | -0.0723 | 1.0433 | 0.9927 | 0.0090 |
| 25 | -0.0632 | 1.0372 | 0.9950 | 0.0074 |
| 26 | -0.0530 | 1.0307 | 0.9969 | 0.0059 |
| 27 | -0.0416 | 1.0237 | 0.9983 | 0.0044 |
| 28 | -0.0291 | 1.0163 | 0.9992 | 0.0029 |
| 29 | -0.0155 | 1.0085 | 0.9998 | 0.0015 |
| 深度/m | b0 | b1 | r | σRES |
|---|---|---|---|---|
| 6 | 0.0115 | 1.0400 | 0.8397 | 0.0706 |
| 7 | 0.2043 | 0.9533 | 0.8293 | 0.0746 |
| 8 | 0.0517 | 1.0146 | 0.8822 | 0.0643 |
| 9 | -0.0085 | 1.0376 | 0.9035 | 0.0598 |
| 10 | -0.0114 | 1.0355 | 0.9186 | 0.0563 |
| 11 | 0.0096 | 1.0238 | 0.9293 | 0.0536 |
| 12 | 0.0215 | 1.0163 | 0.9301 | 0.0543 |
| 13 | -0.0148 | 1.0285 | 0.9456 | 0.0490 |
| 14 | 0.1002 | 0.9785 | 0.9295 | 0.0564 |
| 15 | -0.0640 | 1.0432 | 0.9662 | 0.0401 |
| 16 | -0.0700 | 1.0428 | 0.9669 | 0.0406 |
| 17 | -0.0417 | 1.0282 | 0.9774 | 0.0343 |
| 18 | -0.0501 | 1.0283 | 0.9790 | 0.0338 |
| 19 | -0.0097 | 1.0100 | 0.9842 | 0.0299 |
表 5 基于条件独立方法计算得出的VS(z)—VS[z,20]之间的回归系数、 相关系数及预测误差标准差
Table5 Regression coefficients, correlation coefficients and standard deviations of prediction errors between VS(z)—VS[z,20] calculated based on conditional independence models
| 深度/m | b0 | b1 | r | σRES |
|---|---|---|---|---|
| 6 | 0.0115 | 1.0400 | 0.8397 | 0.0706 |
| 7 | 0.2043 | 0.9533 | 0.8293 | 0.0746 |
| 8 | 0.0517 | 1.0146 | 0.8822 | 0.0643 |
| 9 | -0.0085 | 1.0376 | 0.9035 | 0.0598 |
| 10 | -0.0114 | 1.0355 | 0.9186 | 0.0563 |
| 11 | 0.0096 | 1.0238 | 0.9293 | 0.0536 |
| 12 | 0.0215 | 1.0163 | 0.9301 | 0.0543 |
| 13 | -0.0148 | 1.0285 | 0.9456 | 0.0490 |
| 14 | 0.1002 | 0.9785 | 0.9295 | 0.0564 |
| 15 | -0.0640 | 1.0432 | 0.9662 | 0.0401 |
| 16 | -0.0700 | 1.0428 | 0.9669 | 0.0406 |
| 17 | -0.0417 | 1.0282 | 0.9774 | 0.0343 |
| 18 | -0.0501 | 1.0283 | 0.9790 | 0.0338 |
| 19 | -0.0097 | 1.0100 | 0.9842 | 0.0299 |

图 8 基于条件独立模型建立的不同深度下VS(z)—VS[z,30]拟合回归结果
Fig. 8 Fitting regression results for VS(z)—VS[z,30] at different depths based on conditional independence models.
| 深度/m | b0 | b1 | r | σRES |
|---|---|---|---|---|
| 6 | 0.2134 | 0.9649 | 0.7095 | 0.0641 |
| 7 | 0.3001 | 0.9242 | 0.7545 | 0.0611 |
| 8 | 0.2353 | 0.9492 | 0.8041 | 0.0564 |
| 9 | 0.1656 | 0.9778 | 0.8361 | 0.0530 |
| 10 | 0.2183 | 0.9520 | 0.8606 | 0.0499 |
| 11 | 0.2574 | 0.9337 | 0.8720 | 0.0485 |
| 12 | 0.3053 | 0.9113 | 0.8637 | 0.0506 |
| 13 | 0.3223 | 0.9023 | 0.8653 | 0.0509 |
| 14 | 0.5652 | 0.7979 | 0.8123 | 0.0598 |
| 15 | 0.2208 | 0.9412 | 0.8939 | 0.0465 |
| 16 | 0.2122 | 0.9428 | 0.8917 | 0.0475 |
| 17 | 0.2290 | 0.9341 | 0.8976 | 0.0468 |
| 18 | 0.2287 | 0.9318 | 0.9076 | 0.0450 |
| 19 | 0.2348 | 0.9281 | 0.9236 | 0.0414 |
| 20 | 0.1849 | 0.9464 | 0.9298 | 0.0401 |
| 21 | 0.1626 | 0.9525 | 0.9325 | 0.0397 |
| 22 | 0.0983 | 0.9762 | 0.9447 | 0.0364 |
| 23 | 0.0066 | 1.0110 | 0.9508 | 0.0349 |
| 24 | 0.0262 | 1.0010 | 0.9516 | 0.0351 |
| 25 | 0.0146 | 1.0040 | 0.9575 | 0.0335 |
| 26 | 0.0209 | 0.9999 | 0.9607 | 0.0327 |
| 27 | 0.0178 | 0.9996 | 0.9674 | 0.0303 |
| 28 | 0.0173 | 0.9988 | 0.9717 | 0.0287 |
| 29 | -0.0434 | 1.0215 | 0.9744 | 0.0282 |
表6 基于条件独立模型计算得出的VS(z)—VS[z,30]之间的回归系数、 相关系数及预测误差标准差
Table6 Regression coefficients, correlation coefficients and standard deviations of prediction errors between VS(z)—VS[z,30] calculated based on conditional independence models
| 深度/m | b0 | b1 | r | σRES |
|---|---|---|---|---|
| 6 | 0.2134 | 0.9649 | 0.7095 | 0.0641 |
| 7 | 0.3001 | 0.9242 | 0.7545 | 0.0611 |
| 8 | 0.2353 | 0.9492 | 0.8041 | 0.0564 |
| 9 | 0.1656 | 0.9778 | 0.8361 | 0.0530 |
| 10 | 0.2183 | 0.9520 | 0.8606 | 0.0499 |
| 11 | 0.2574 | 0.9337 | 0.8720 | 0.0485 |
| 12 | 0.3053 | 0.9113 | 0.8637 | 0.0506 |
| 13 | 0.3223 | 0.9023 | 0.8653 | 0.0509 |
| 14 | 0.5652 | 0.7979 | 0.8123 | 0.0598 |
| 15 | 0.2208 | 0.9412 | 0.8939 | 0.0465 |
| 16 | 0.2122 | 0.9428 | 0.8917 | 0.0475 |
| 17 | 0.2290 | 0.9341 | 0.8976 | 0.0468 |
| 18 | 0.2287 | 0.9318 | 0.9076 | 0.0450 |
| 19 | 0.2348 | 0.9281 | 0.9236 | 0.0414 |
| 20 | 0.1849 | 0.9464 | 0.9298 | 0.0401 |
| 21 | 0.1626 | 0.9525 | 0.9325 | 0.0397 |
| 22 | 0.0983 | 0.9762 | 0.9447 | 0.0364 |
| 23 | 0.0066 | 1.0110 | 0.9508 | 0.0349 |
| 24 | 0.0262 | 1.0010 | 0.9516 | 0.0351 |
| 25 | 0.0146 | 1.0040 | 0.9575 | 0.0335 |
| 26 | 0.0209 | 0.9999 | 0.9607 | 0.0327 |
| 27 | 0.0178 | 0.9996 | 0.9674 | 0.0303 |
| 28 | 0.0173 | 0.9988 | 0.9717 | 0.0287 |
| 29 | -0.0434 | 1.0215 | 0.9744 | 0.0282 |
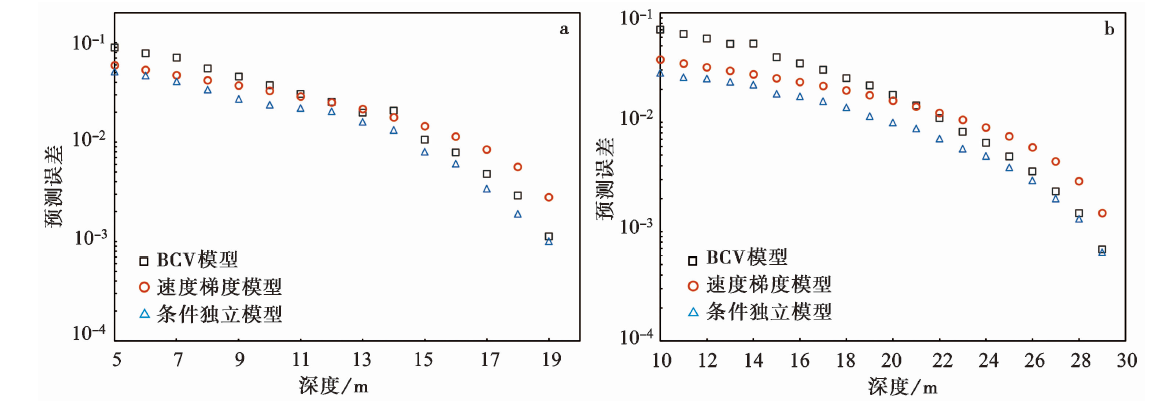
图 9 采用3种方法建立的山东地区VS20(a)和VS30(b)经验外推模型的误差对比
Fig. 9 Comparison of the errors of the VS20(a) and VS30 (b) prediction models built using the three models for the Shandong province.
| [1] |
薄景山, 李秀领, 李山有. 2003. 场地条件对地震动影响研究的若干进展[J]. 世界地震工程, 19(2): 11—15.
|
|
|
|
| [2] |
陈国兴, 丁杰发, 方怡, 等. 2020. 场地类别分类方案研究[J]. 岩土力学, 41(11): 3509—3522.
|
|
|
|
| [3] |
翠川三郎, 野木淑裕. 2015. 深さ30mまでの地盤の平均S波速度を深さの浅いデータから推定する方法について[J]. 日本地震工学会論文集, 15(2): 91—96.
|
|
|
|
| [4] |
党鹏飞, 刘启方. 2019. 新疆乌鲁木齐地区VS30 经验估计研究[J]. 地震工程学报, 41(5): 1324—1331.
|
|
|
|
| [5] |
刁守中. 2009. 20世纪山东10大地震[M]. 北京: 地震出版社.
|
|
|
|
| [6] |
葛孚刚, 王冬雷, 许洪泰, 等. 2020. 山东地区等效剪切波速与30m等效剪切波速转换研究[J]. 科学技术与工程, 20(24): 9751—9756.
|
|
|
|
| [7] |
贺为民, 刘明军, 杨杰. 2016. 土层剪切波速与埋深关系统计分析和应用[J]. 地震地质, 38(4): 937—949. doi: 10.3969/j.issn.0253-4967.2016.04.011.
|
|
|
|
| [8] |
侯兴民, 薄景山, 杨学山, 等. 2004. 互相关函数在单孔法剪切波速测量中的应用[J]. 地震工程与工程振动, 24(2): 59—63.
|
|
|
|
| [9] |
黄雅虹, 吕悦军, 兰景岩, 等. 2010. 工程场地分类中等效剪切波速计算深度问题的讨论[J]. 地震地质, 32(2): 312—319. doi: 10.3969/j.issn.0253-4967.2010.02.014.
|
|
|
|
| [10] |
贾琳, 谢俊举, 李小军, 等. 2021. 四川和云南地区场地平均剪切波速VS20 和VS30 经验预测模型研究[J]. 地震学报, 43(5): 628—642, 679.
|
|
|
|
| [11] |
蒋其峰, 魏玮, 王红卫, 等. 2017. 山东省场地类别分布及地震动峰值加速度区划调整[J]. 震灾防御技术, 12(3): 501—510.
|
|
|
|
| [12] |
江志杰, 彭艳菊, 方怡, 等. 2018. 北京平原地区VS30 估算模型适用性研究[J]. 震灾防御技术, 13(1): 75—86.
|
|
|
|
| [13] |
李洪奎, 于学峰, 耿科, 等. 2012. 山东省大地构造相研究[M]. 北京: 地质出版社.
|
|
|
|
| [14] |
李敏, 杨立国, 陈海鹏, 等. 2020. 杭州市典型土层剪切波速与埋深间的关系分析[J]. 震灾防御技术, 15(1): 77—88.
|
|
|
|
| [15] |
李小军. 2013. 地震动参数区划图场地条件影响调整[J]. 岩土工程学报, 35(S2): 21—29.
|
|
|
|
| [16] |
鹿子林, 付海清, 胡超, 等. 2014. 钻孔剪切波速测试2种方法的对比[J]. 华北地震科学, 32(2): 45—49.
|
|
|
|
| [17] |
吕悦军, 彭艳菊, 兰景岩, 等. 2008. 场地条件对地震动参数影响的关键问题[J]. 震灾防御技术, 3(2): 126—135.
|
|
|
|
| [18] |
米欣雪, 张雨婷, 任叶飞, 等. 2023. 一种场地VS30 经验估计最佳模型的选用方法: 以新疆地区为例[J]. 西安建筑科技大学学报(自然科学版), 55(2): 288—292.
|
|
|
|
| [19] |
彭艳菊, 吕悦军, 黄雅虹, 等. 2009. 工程地震中的场地分类方法及适用性评述[J]. 地震地质, 31(2): 349—362. doi: 10.3969/j.issn.0253-4967.2009.02.016.
|
|
|
|
| [20] |
宋明春. 2008. 山东省大地构造格局和地质构造演化[D]. 北京: 中国地质科学院.
|
|
|
|
| [21] |
王大任, 任叶飞, 张雨婷, 等. 2023. 一种建筑工程场地参数VS30 的外推模型修正方法[J]. 哈尔滨工业大学学报, 55(9): 1—6.
|
|
|
|
| [22] |
王红卫, 冯志军, 刘希强, 等. 2015. 山东地区地震动峰值加速度场地效应的定量分析[J]. 地震地质, 37(1): 44—52. doi: 10.3969/j.issn.0253-4967.2015. 01.004.
|
|
|
|
| [23] |
王志才, 贾荣光, 孙昭民, 等, 2005. 沂沭断裂带安丘-莒县断裂安丘—朱里段几何结构与活动特征[J]. 地震地质, 27(2): 212—220.
|
|
|
|
| [24] |
王志才, 王冬雷, 许洪泰, 等. 2015. 安丘-莒县断裂北段几何结构与最新活动特征[J]. 地震地质, 37(1): 176—191. doi: 10.3969/j.issn.0253-4967.2015.01.014.
|
|
|
|
| [25] |
喻畑, 李小军. 2015. 四川、 甘肃地区VS30 经验估计研究[J]. 地震工程学报, 37(2): 525—533.
|
|
|
|
| [26] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 2016. 建筑抗震设计规范(GB50011- 2010)[S]. 北京: 中国建筑工业出版社: 18—20.
|
|
Ministry of Housing and Urban-rural Development of the People's Republic of China,General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. 2016. Code for Seismic Design of Buildings(GB50011-2010)[S]. China Architecture & Building Press, Beijing:18—20. (in Chinese)
|
|
| [27] |
周健, 李小军, 李亚琦, 等. 2021. 中美建筑抗震设计规范中工程场地类别的对比和换算关系[J]. 地震学报, 43(4): 521—532, 534.
|
|
|
|
| [28] |
|
| [29] |
|
| [30] |
Building Seismic Safety Council(BSSC).2020. NEHRP recommended seismic provisions for new buildings and other structures[S]. Washington DC.
|
| [31] |
|
| [32] |
European Committee for Standardization. 2014. EUROCODE 8: Design of structures for earthquake resistance Part 1: General rules, seismic actions and rules for buildings [S]. London.
|
| [33] |
|
| [34] |
|
| [35] |
|
| [1] | 黄雅虹, 吕悦军, 兰景岩, 施春花, 史丙新. 工程场地分类中等效剪切波速计算深度问题的讨论[J]. 地震地质, 2010, 32(2): 312-319. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||